Flow-base

Flow 的核心思路是找到一个从简单先验分布映射到训练数据所在分布的函数，其结构如下图所示：

相对于 VAE 预设对象的密度分布是连续的所以把先验分布映射到一个简单的隐变量分布上，然后使用 decoder 从隐变量空间学习还原生成后验分布来说，flow 采用一个简单粗暴但在数学上极具美感的做法，它采用一个可逆的方法对先验分布进行学习，暴力的学习先验空间到简单分布的映射，之后用逆方法对其进行生成。个人感觉其相当于把 VAE 的 encoder 和 decoder 揉到一起去了，采用了可逆函数的特点简化了 encoder 和 decoder 对过程。

生成器

Flow 模型旨在学习一个可逆变换函数 G，该函数将一个简单的先验分布（通常是高斯分布）z 映射到数据分布 x：

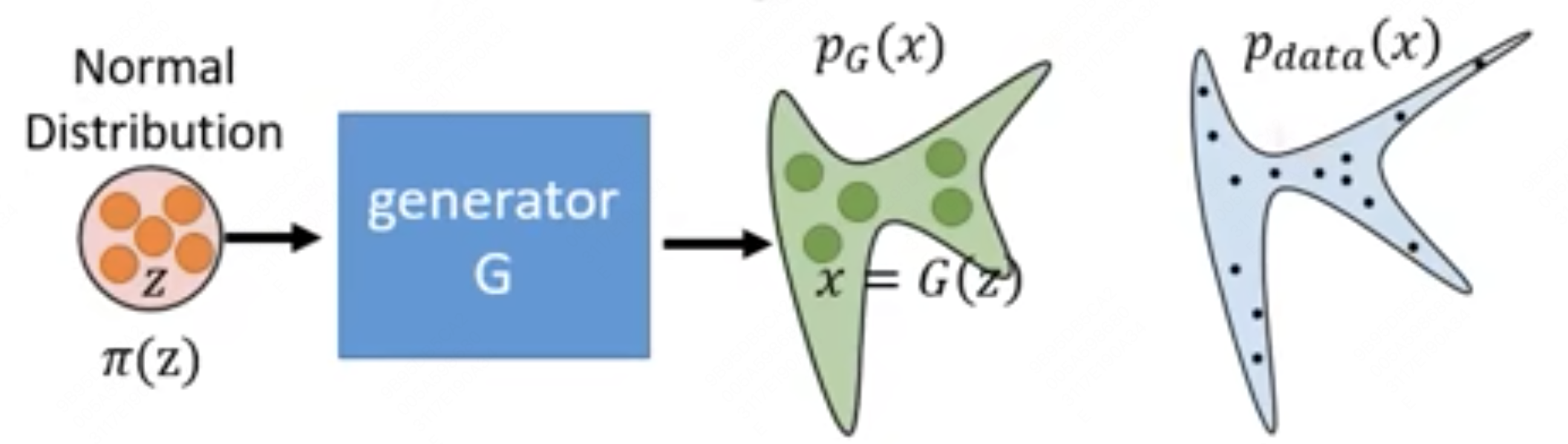
Untitled

$$ x = G(z) $$

由于 G 是可逆的，我们可以得到逆变换：

$$ z = G⁻¹(x) $$

这种可逆性是 Flow 模型的关键，它允许我们直接计算数据 x 的概率密度：

$$ p(x)=\pi (z)\left|\det J_{G^{-1}} \right| $$

其中 $p(z)$ 是先验分布的概率密度，$J_{G^{-1}}$ 是逆变换 $G⁻¹$ 的雅可比矩阵。

flow 优化真实值在后验分布中的最大似然，公式如下：

$$ G^*=arg max \displaystyle\sum^m_{i=1}logP_G(x_i) $$

Change of variable Theorem

$$ p(x') = \pi(z') \left| \frac{dz}{dx} \right| $$

$$ p(x') \left| \det \begin{bmatrix} \Delta x_{11} & \Delta x_{21} \\ \Delta x_{12} & \Delta x_{22}\end{bmatrix} \right| = \pi(z') \Delta z_{1} \Delta z_{2} $$$$ p(x')=\pi (z')\left|\det J_{f^{-1}} \right| $$

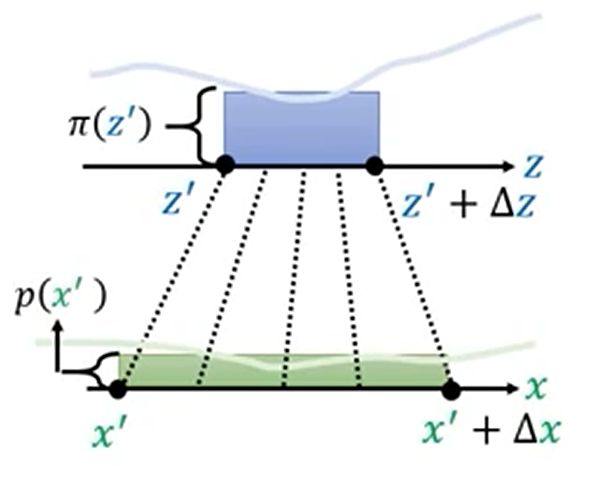
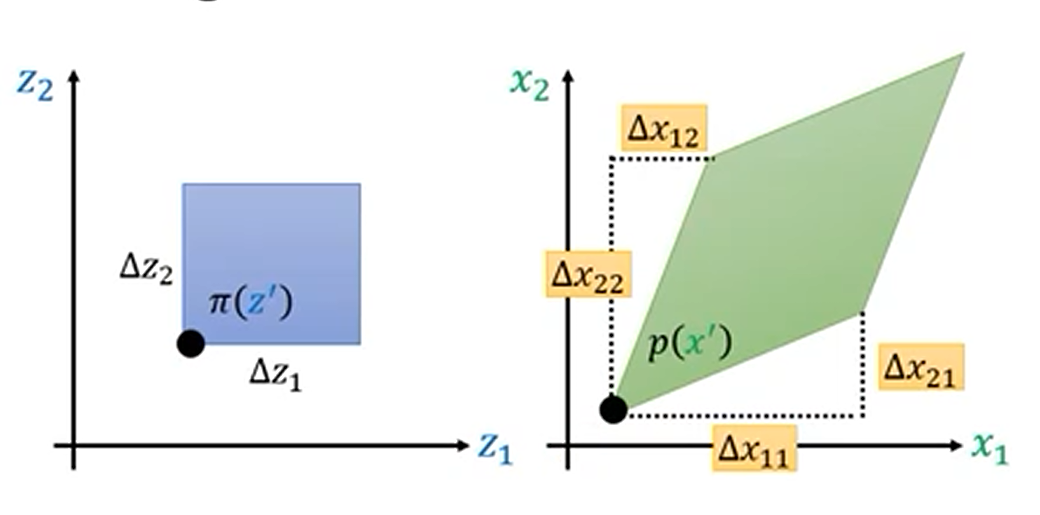
Jabobian 矩阵

Jacobian 矩阵是一个函数的所有一阶偏导数的矩阵。对于从$R^n$映射到$R^m$的函数，Jacobian 矩阵的维度是$m \times n$。

对于函数 $F: R^n \rightarrow R^m$，其中 $F(x) = [f_1(x), f_2(x), …, f_m(x)]^T$， Jacobian 矩阵 J 表示为：

$$ J = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix} $$

几何意义

线性逼近： 雅可比矩阵代表了函数 f 在给定点 x 的最佳线性逼近。也就是说，当 x 发生一个微小变化 Δx 时，f(x) 的变化 Δf 可以近似表示为：

$$ Δf ≈ J Δx $$

这个公式类似于单变量微积分中的导数概念，雅可比矩阵相当于多变量函数的“导数”。

局部变换： 雅可比矩阵描述了函数 f 在 x 附近的局部变换。它反映了输入空间的微小变化如何在输出空间中被拉伸、压缩或旋转。
体积变化： 雅可比矩阵的行列式 $|det(J)|$ (当 $m = n$ 时，雅可比矩阵为方阵) 表示函数 $f$ 在 $x$ 附近对体积的改变程度。如果 $|det(J)| > 1$，则表示体积被放大；如果 $0 < |det(J)| < 1$，则表示体积被缩小；如果 $|det(J)| = 0$，则表示变换将输入空间映射到一个低维空间。

Flow-base

最终的优化目标是$P_G(x_i)$，由上式可知：

$$ p(x)=\pi(\mathbb{G}^{-1}(x))\left|\det J_{\mathbb{G}^{-1}} \right| $$

两边取对数可得：

$$ \log p_{\mathbb{G}}(x) = \log \pi(\mathbb{G}^{-1}(x)) + \log |det(J_{\mathbb{G}^{-1}})| $$

Coupling Layer

为了解决生成器可逆的问题，flow 采用了如下结构的生成器

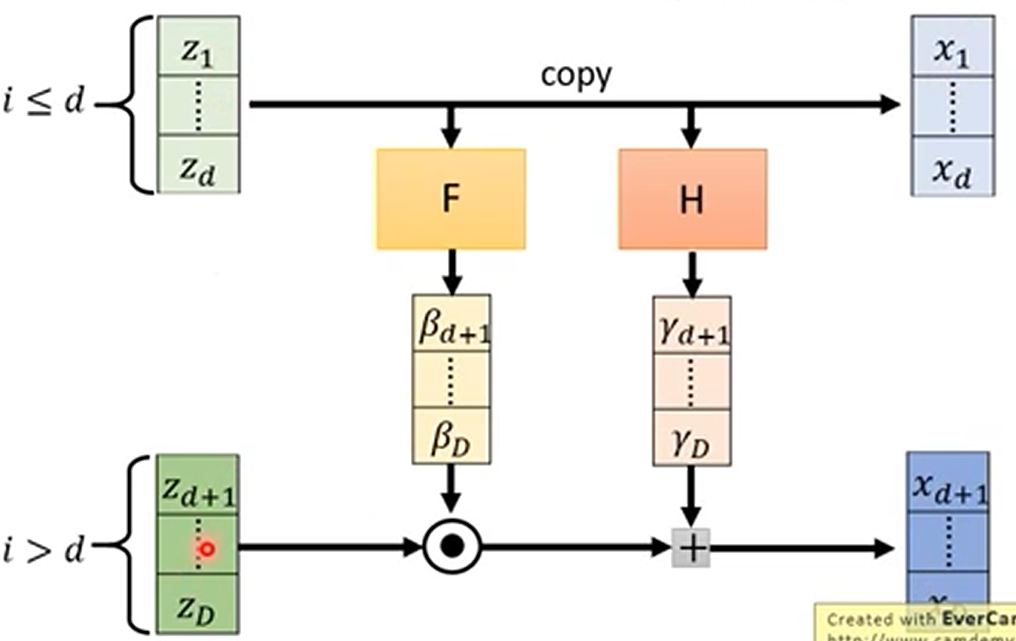
其中，分别讲输出和输出分成两个部分，对于对于原函数计算，我们将第一个部分直接复制，然后通过两个神经网络得到$\beta$和$\gamma$，然后通过$x=z\cdot \beta + \gamma$计算$x$值。反函数的计算直接复制第一部分，第二个部分相减即可

解决了生成器的反函数问题，优化最大似然的目标就是找到生成器的 Jabobian 矩阵，生成器的 Jabobian 矩阵计算如下：

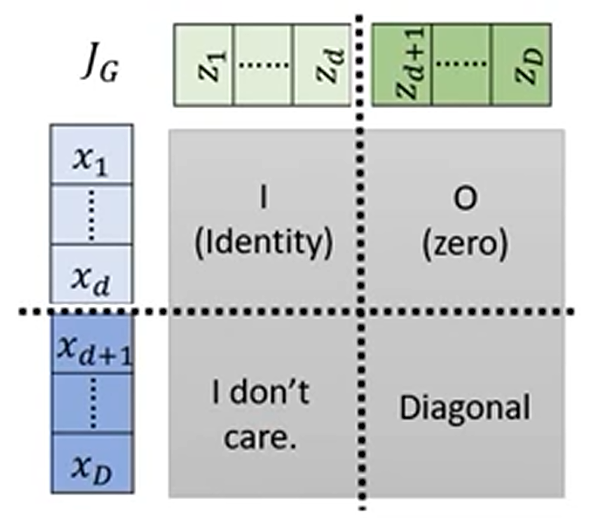
对于第一个部分，易知其为单位矩阵，$z$的第二部分和第一部分无关，所以为零矩阵，此时整个函数的 Jabobian 矩阵只与右下角这一部分有关，右下角部分逐个求偏导就是$\beta$的值，故整个函数的 Jabobian 矩阵可写作如下形式：

$$ ⁍ $$

Coupling Layer-Stacking

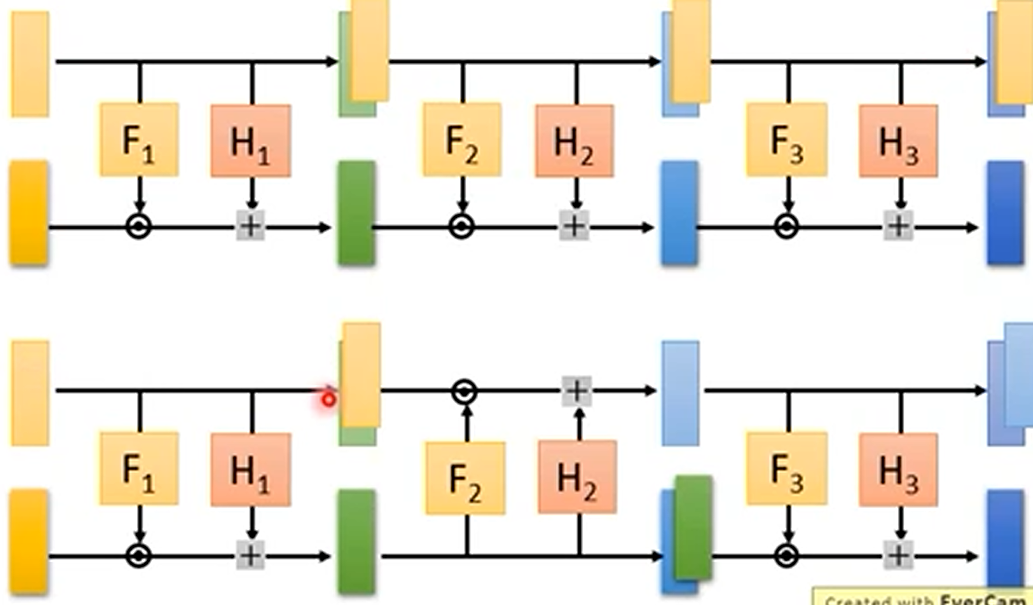
我们通常将多个 flow 模型堆叠起来进行使用，这会产生一个问题：每次只有二部分参与变换，所以我们采用 Coupling Layer-Stacking，也就是每次生成器会切换不同的部分进行变换。