计算机组成原理复习

第一章计算机系统概论

计算机发展历程

计算机的四代发展

第一代(1945-1955)
- 特征:电子管、插板式编程
- 编程方式:机器语言
- 主要用途:数值计算
第二代(1955-1965)
- 特征:晶体管、批处理系统
- 编程方式:汇编语言、FORTRAN
- 代表机型:IBM 7094
第三代(1965-1980)
- 特征:集成电路、多道程序、分时系统
- 编程方式:高级语言(BASIC、C)
- 技术创新:多道程序设计、分时处理
第四代(1980-至今)
- 特征:超大规模集成电路
- 发展方向:
  - 个人计算机
  - 并行计算
  - 分布式系统
  - 云计算

计算机系统的层次结构

计算机系统的五个层次

高级语言层(M4)
汇编语言层(M3)
操作系统层(M2)
机器语言层(M1)
微程序层(M0)

性能指标

主要性能指标

CPI(Cycles Per Instruction)

基本公式 / Basic Formula
- 中文：CPI = 总时钟周期数 / 总指令数
- English: CPI = Total Clock Cycles / Total Instructions
表示为数学公式 / Mathematical expression: $CPI=\frac{Clock Cycles}{Instruction Count}$
加权平均公式 / Weighted Average Formula

当有多种类型的指令时 / When there are multiple instruction types:

$CPI=\sum_{i=1}^{n}(CPI_i×F_i)$

MIPS(Million Instructions Per Second)

基本公式 / Basic Formula

$MIPS=\frac{指令数执行}{时间×10^6}=\frac{时钟频率}{CPI×10^6}$

英文表示 / In English: $MIPS=\frac{Instruction Count}{Execution Time×10^6}=\frac{Clock Frequency}{CPI×10^6}$

扩展公式 / Extended Formula

当已知时钟频率（Hz）和CPI时：/ When clock frequency (Hz) and CPI are known:

$MIPS=\frac{Clock Frequency (Hz)}{CPI×10^6}$

重要例题分析

例题1: CPI计算

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


问题:某程序的目标代码由4类指令组成:
- 算术逻辑运算(60%, CPI=1)
- 内存读写(18%, CPI=2)
- 转移(12%, CPI=4)
- 其它(10%, CPI=8)
求该程序的平均CPI。

解答:
CPI = 1×0.6 + 2×0.18 + 4×0.12 + 8×0.1
    = 0.6 + 0.36 + 0.48 + 0.8
    = 2.24

例题2: CPU性能计算

$$ N=t\times f $$

N：时钟周期总数
t：运行时间
f：频率

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


问题:程序P在机器A上运行需10s,机器A的时钟频率为400MHz。
如果在机器B上运行只需6s,且B的时钟周期总数是A的1.2倍,
求B的时钟频率是A的多少倍?

解答:
1. 计算A的时钟周期总数:
   时钟周期总数A = 10s × 400MHz = 4000M个

2. 计算B的时钟频率:
   时钟频率B = (1.2 × 4000M) ÷ 6s = 800MHz

3. 比值 = 800MHz ÷ 400MHz = 2倍

例题3: MIPS计算

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


问题：
某计算机系统运行一个程序，CPU时钟频率2GHz，执行了5×10⁸条指令，平均CPI为2.5，
程序总执行时间0.625秒。
求：(1)该程序的MIPS值；
		(2)若CPU频率提高到2.5GHz，新的MIPS值是多少？

解：
(1) MIPS = 指令数/(执行时间×10⁶) = 5×10⁸/(0.625×10⁶) = 800

(2) 新执行时间 = 原执行时间×(原频率/新频率) = 0.625×(2/2.5) = 0.5s
新MIPS = 5×10⁸/(0.5×10⁶) = 1000

冯·诺依曼计算机的基本特点

五大部件
- 运算器(ALU)
- 控制器(CU)
- 存储器(Memory)
- 输入设备(Input)
- 输出设备(Output)
重要特征
- 计算机由五大部件组成
- 指令和数据以二进制表示
- 指令和数据存放在同一存储器中
- 指令由操作码和地址码组成
- 存储程序
- 按地址访问

第二章计算机数据表示

数据表示基础

为什么使用二进制

易于实现：只有0和1两种状态
抗干扰能力强
便于逻辑运算
硬件实现简单

数据表示考虑因素

数据类型（数值/非数值）
表示范围和精度
存储和处理代价
软件可移植性

数值数据表示

机器数的编码方式

原码
反码
补码
移码

原码

最高位为符号位（0正1负）
其余位是数值的绝对值
公式：
$$ [X]_{\text{原}} = \begin{cases} X, & 0 \leq X < 2^n \\ 2^n - |X|, & -2^n < X \leq 0 \end{cases} $$

反码

正数的反码与原码相同
负数的反码是对原码除符号位外各位取反
公式：
$$ [X]_{\text{反}} = \begin{cases} X, & 0 \leq X < 2^n \\ 2^{n+1}-1 + X, & -2^n < X \leq 0 \end{cases} $$

补码

正数的补码与原码相同
负数的补码是在反码的基础上末位加1
公式：
$$ [X]_{\text{补}} = \begin{cases} X, & 0 \leq X < 2^n \\ 2^{n+1} + X, & -2^n < X \leq 0 \end{cases} $$

移码

常用于表示浮点数的阶码
公式： $[x]_移 = x + 2^{n-1}$
与补码的关系：符号位取反其余位不变

例题

示例1：将十进制数 +52 转换为8位二进制机器码

原码
- 正数，符号位为0
- 52的二进制为110100
- 8位原码表示：0110,1000
反码
- 正数的反码等于原码
- 所以反码也是：0110,1000
补码
- 正数的补码等于原码
- 所以补码也是：0110,1000

示例2：将十进制数 -52 转换为8位二进制机器码

原码
- 负数，符号位为1
- |52|的二进制为110100
- 8位原码表示：1110,1000
反码
- 负数，符号位为1
- 数值位按位取反
- 计算过程
  1 2
  
  原码：1110,1000 数值位取反：1001,0111
补码
- 负数，在反码基础上末位加1
- 计算过程
  1 2
  
  反码：1001,0111 末位加1：1001,1000

转换口诀

正数：原码 = 反码 = 补码
负数：
- 原码：符号位为1，其余为绝对值的二进制
- 反码：符号位为1，数值位按位取反
- 补码：反码末位加1

整型和浮点型表示

整型

整型在计算机中使用补码表示

1
2
3
4
5


类型      位数    范围
byte      8位    -128 到 127
short     16位   -32,768 到 32,767
int       32位   -2^31 到 2^31-1
long      64位   -2^63 到 2^63-1

浮点数

$$ V=(-1)^s \times M \times 2^E $$

其中：

S：符号位（0正1负）
M：1.尾数（规范化的尾数）
E：指数值（减去偏置值的指数）

例子：存储float类型的12.375

转换为二进制：

1
2
3


12 = 1100(二进制)
0.375 = 0.011(二进制)
12.375 = 1100.011(二进制)

规范化：
1

1100.011 = 1.100011 × 2^3

存储格式：

1
2
3
4
5


符号位(S)：0（正数）
指数位(E)：3 + 127(偏置) = 130 = 10000010
尾数位(M)：100011（不存储小数点前的1）

最终存储：0 10000010 10001100000000000000000

字节序

大端序(Big Endian)：高位字节存储在低地址
小端序(Little Endian)：低位字节存储在低地址

1
2
3


例如：整数 0x12345678
大端序：12 34 56 78
小端序：78 56 34 12

数据校验

码距

码距是指两个等长编码之间不同位的个数
最小码距是指一个编码系统中任意两个合法编码之间的最小距离

1
2
3
4


例如：
编码A：1 0 1 1 0
编码B：1 1 1 0 0
码距 = 2（第2位和第4位不同）

奇偶校验

偶校验 / Even Parity

原理：确保数据位中"1"的总数（包括校验位）为偶数
校验位设置：如果数据位中"1"的个数为奇数，则校验位设为1；如果为偶数，则设为0

奇校验 / Odd Parity

原理：确保数据位中"1"的总数（包括校验位）为奇数
校验位设置：如果数据位中"1"的个数为偶数，则校验位设为1；如果为奇数，则设为0

海明码

校验码位置

校验位放在2的幂次位置上（1,2,4,8,…）
数据位放在其他位置上

1
2
3


位置：  1  2  3  4  5  6  7  8  9  10 11
类型：  p1 p2 d1 p3 d2 d3 d4 p4 d5 d6 d7
(p=校验位, d=数据位)

校验码数量

对于k位数据，需要r位校验位，满足：

$$ 2^r ≥ k + r + 1 $$

校验码负责校验的位置

p1(位置1): 检查二进制第1位为1的位置

1

001(1), 011(3), 101(5), 111(7)

p2(位置2): 检查二进制第2位为1的位置

1

010(2), 011(3), 110(6), 111(7)

p3(位置4): 检查二进制第3位为1的位置

1

100(4), 101(5), 110(6), 111(7)

校验码的值

校验码就是在负责校验位置上的偶校验

对单个错误进行纠错

计算综合征

第一位综合征(s1)
- 检查所有奇数位置的位
- s1 = p1 ⊕ d1 ⊕ d2 ⊕ d4
第二位综合征(s2)
- 检查位置2,3,6,7的位
- s2 = p2 ⊕ d1 ⊕ d3 ⊕ d4
第三位综合征(s3)
- 检查位置4,5,6,7的位
- s3 = p3 ⊕ d2 ⊕ d3 ⊕ d4

以此类推

综合征含义

1
2
3
4
5
6
7
8
9


综合征值(s3s2s1)  表示含义
000              无错误
001              位置1出错
010              位置2出错
011              位置3出错
100              位置4出错
101              位置5出错
110              位置6出错
111              位置7出错

以此类推

例题海明码实例：4位数据的(7,4)海明码

原始数据

假设要传输的数据是：1011

生成海明码

确定位置

1
2
3
4
5


位置：    1   2   3   4   5   6   7
用途：    p1  p2  d1  p3  d2  d3  d4
数据：    p1  p2  1   p3  0   1   1
         ^   ^   ^   ^   ^   ^   ^
二进制：  001 010 011 100 101 110 111

计算校验位
1. 计算p1（检查1,3,5,7位）
  - p1 ⊕ d1 ⊕ d2 ⊕ d4 = 0
  - p1 ⊕ 1 ⊕ 0 ⊕ 1 = 0
  - p1 = 1 ⊕ 0 ⊕ 1 = 0
2. 计算p2（检查2,3,6,7位）
  - p2 ⊕ d1 ⊕ d3 ⊕ d4 = 0
  - p2 ⊕ 1 ⊕ 1 ⊕ 1 = 0
  - p2 = 1 ⊕ 1 ⊕ 1 = 1
3. 计算p3（检查4,5,6,7位）
  - p3 ⊕ d2 ⊕ d3 ⊕ d4 = 0
  - p3 ⊕ 0 ⊕ 1 ⊕ 1 = 0
  - p3 = 0 ⊕ 1 ⊕ 1 = 0

最终海明码

1
2


位置：    1   2   3   4   5   6   7
数据：    0   1   1   0   0   1   1

完整的海明码是：0110011

错误检测示例

3.1 假设第5位发生错误

接收到的错误数据：0110111（第5位从0变成了1）

3.2 计算综合征
1. 计算s1（检查1,3,5,7位）
  - 0 ⊕ 1 ⊕ 1 ⊕ 1 = 1
2. 计算s2（检查2,3,6,7位）
  - 1 ⊕ 1 ⊕ 1 ⊕ 1 = 0
3. 计算s3（检查4,5,6,7位）
  - 0 ⊕ 1 ⊕ 1 ⊕ 1 = 1
3.3 错误定位
- 得到的综合征：101
- 对照综合征表：101 表示第5位出错
- 将第5位取反即可纠正错误
3.4 纠错结果
1 2 3

错误数据： 0 1 1 0 1 1 1 纠正后： 0 1 1 0 0 1 1 位置： 1 2 3 4 5 6 7
验证正确性

4.1 重新检验

计算三个校验方程：
1. s1 = 0 ⊕ 1 ⊕ 0 ⊕ 1 = 0
2. s2 = 1 ⊕ 1 ⊕ 1 ⊕ 1 = 0
3. s3 = 0 ⊕ 0 ⊕ 1 ⊕ 1 = 0
所有校验方程结果都为0，说明纠错成功。

4.2 提取原始数据
- 取出数据位（第3,5,6,7位）：1011
- 与原始数据相同，验证成功

CRC循环冗余校验

校验流程

确定CRC位数（r）

应满足：$2^r>数据长度+r$
选择合适的CRC标准
1. CRC-16
  - 生成多项式：$x^{16}+x^{15}+x^{2}+1$
  - 广泛应用于USB、Modbus等协议
2. CRC-32
  - 生成多项式：$x^{32}+x^{26}+x^{23}+x^{22}+x^{16}+x^{12}+x^{11}+x^{10}+x^{8}+x^7+x^5+x^4+x^2+x+1$
  - 用于以太网、ZIP文件等
3. CRC-8
  - 生成多项式：$x^8+x^7+x^6+x^4+x^2+1$
  - 用于简单的数据校验
4. CRC-4
  - 生成多项式：$x^3+x+1$
数据预处理

补零操作（补生成多项式度数-1个零），并接到原数据后面
求余数

用补完0的数除以生成多项式的二进制表示来求得余数，并将余数替换后面补的0
判断是否正确

通过传入的数除以CRC方法对应的多项式来判断是否正确，余0表示正确

CRC循环校验的优势和劣势

优势

能够检测所有单比特错误
能够检测所有双比特错误
能够检测大多数突发错误
能检测所有奇数个数错误

劣势

无法纠错
存在理论上的盲区

例题 CRC计算

题目：数据1100，生成多项式G(x)=1011，求CRC码。

步骤：

数据左移3位：1100000

模2除法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


1100000÷1011
1011
-----
1110
1011
-----
1010
1011
-----
0010 (余数)

CRC码：1100010

第三章运算方法与运算器

定点加减法运算

补码加法运算 (Addition in Two’s Complement)

补码的加法非常直接，直接按位相加，溢出位舍弃。 Addition in two’s complement is straightforward - add bits directly and discard overflow.

例如 (Example)：

1
2
3
4


  5 的补码 (TC of 5):  0101
 -3 的补码 (TC of -3): 1101
 -------------------------
 相加结果 (Sum):       0010 (= 2)

补码减法运算 (Subtraction in Two’s Complement)

减法可以转换为加上负数的补码：A - B = A + (-B) Subtraction can be converted to adding the two’s complement of the negative number: A - B = A + (-B)

例如 (Example)：

1
2
3
4
5
6


5 - 3 = 5 + (-3)

  5 的补码 (TC of 5):  0101
 -3 的补码 (TC of -3): 1101
 -------------------------
 结果 (Result):        0010 (= 2)

溢出检测 (Overflow Detection)

正溢出 (Positive Overflow)

两个正数相加，结果变成负数 When adding two positive numbers results in a negative number
负溢出 (Negative Overflow)

两个负数相加，结果变成正数 When adding two negative numbers results in a positive number

检测方法 (Detection Methods)

符号位进位法 (Sign Bit Carry Method)

观察最高位的进位和最高位前一位的进位，如果不同则发生溢出 Compare the carry into and out of the sign bit - if different, overflow occurred
符号位检查法 (Sign Bit Check Method)

检查两个操作数符号相同，但结果符号不同 Check if operands have the same sign but result has different sign

补码的加减法示例 (Examples)

让我们看一个具体的8位补码计算示例： Let’s look at an 8-bit two’s complement calculation example:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


1. 计算 5 + (-3)：
   Calculate 5 + (-3):

   5:     00000101
   -3:    11111101
   ----------------
   结果:   00000010 (= 2)

2. 计算 -5 - 3 = -5 + (-3)：
   Calculate -5 - 3 = -5 + (-3):

   -5:    11111011
   -3:    11111101
   ----------------
   结果:   11110110 (= -8)

定点乘法运算

原码乘法运算

原码乘法运算和手算乘法的程序一样，都是各位相乘以后相加，不多做赘述

补码乘法运算（Booth算法）

补码乘法运算遵循以下法则：

对于乘数$x$被乘数$y$，分别求$[x]_补$、$[-x]_补$、$[y]_补$
初始化$A=0$，$Q=[y]补$，$Q{-1}=0$
进行如下循环操作：
1. 比较Q0和Q(-1)，根据结果进行操作：
  - 若$Q_0Q_{-1}=00或11$，$AQQ_{-1}$右移
  - 若$Q_0Q_{-1}=10$，$AQQ_{-1}$加$[-x]$后右移
  - 若$Q_0Q_{-1}=01$，$AQQ_{-1}$加$[x]$后右移
2. 操作次数等于乘数的数值位数（不包括符号位）
3. 最后将$A$和$Q$拼接起来

补码乘法小数位置确定

两个n位小数相乘，结果为2n位小数
小数点应放在最高位之前
结果的精度是原始数精度的两倍

定点除法运算

原码除法运算

恢复余数除法

感觉原码直接打竖式算就可以了

对于被除数$x$和除数$y$，分别求$|x|$、$|x|_补$、$|y|_补$、$[-y]_补$
用$|x|_补+[-y]_补$，做如下判断
1. 若结果为正，商1，左移
2. 若结果为负，商0，$+[y]_补$，恢复后左移
重复上述操作直到商和机器码长度一致
最后的余数要乘以$2^{左移次数}$

补码的除法运算

符号位参与运算
被除数、除数、余数采用双符号位

运算步骤

对于被除数$x$和除数$y$，分别求$|x|$、$|y|_补$、$|-y|_补$
首先判被除数（$x_补$）与除数（$y_补$）是同号还是异号.如果是同号,就要减去（$y_补$）.如果是异号就要加上（$y_补$）.
算出的余数再与除数（$y_补$）进行比较:
- 如果是同号,商上1,向左移动一位,再减去（$y_补$）,加上（$[-y]_补$）
- 如果是异号,商上0,向左移动一位,再加上（$y_补$）
循环操作第三步直到商的位数和机器码相同
补码除法的商最后一位固定设置为1
将余数乘以$2^{左移次数}$

浮点数加减法

运算步骤

对阶 Alignment
- 将小指数的数向大指数对齐
- 小指数数的尾数右移，每右移一位，指数加1
- 直到两个数的指数相等
尾数运算 Mantissa Operation
- 对阶后进行尾数的加减运算
- 注意保持正确的符号
规格化 Normalization
- 调整结果使其满足规格化要求
- 通常要求尾数最高位为1
- 可能需要左移或右移尾数
舍入 Rounding
- 根据舍入规则处理多余的位
溢出检查 Overflow Check
- 检查结果是否超出表示范围

示例 Examples

例1：基本加法 Basic Addition

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


计算：1.101×2² + 1.001×2¹

1. 对阶：
   1.101×2² = 1.101×2²
   1.001×2¹ = 0.1001×2²  (右移一位)

2. 尾数相加：
   1.101
   0.1001
   -------
   10.0011×2²

3. 规格化：
   1.00011×2³

4. 舍入（假设4位精度）：
   1.000×2³

例2：异号加法（实质是减法）Subtraction

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


计算：1.110×2³ - 1.101×2²

1. 对阶：
   1.110×2³ = 1.110×2³
   1.101×2² = 0.110×2³  (右移一位)

2. 尾数相减：
   1.110
   0.110
   -------
   1.000×2³

特殊情况 Special Cases

上溢 Overflow

1
2


当结果超过最大可表示范围时发生
例如：1.111×2¹²⁷ + 1.111×2¹²⁷

下溢 Underflow

1
2


当结果小于最小可表示范围时发生
例如：1.000×2⁻¹²⁶ ÷ 2

精度损失 Precision Loss

1
2
3


当两个数量级相差很大时：
1.234×2²⁰ + 1.234×2⁻²⁰
小的数可能完全被忽略

运算方法与运算器

半加法器（Half Adder HA）

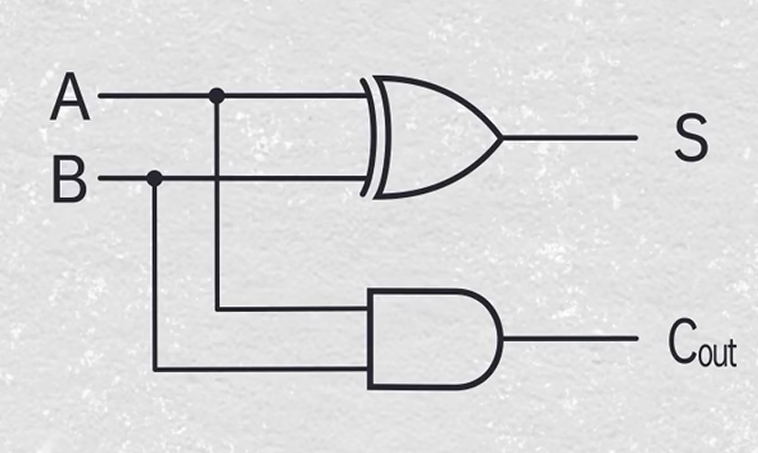
全加法器（Full Adder FA）

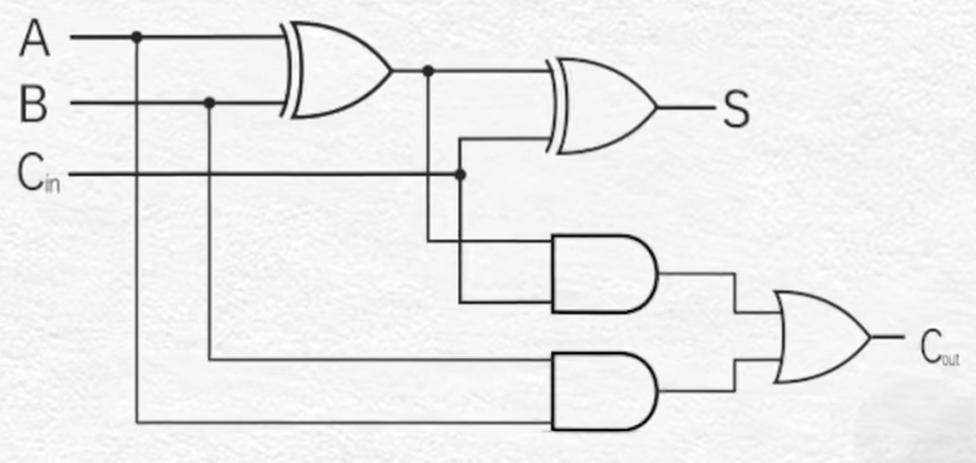
串行进位全加法器

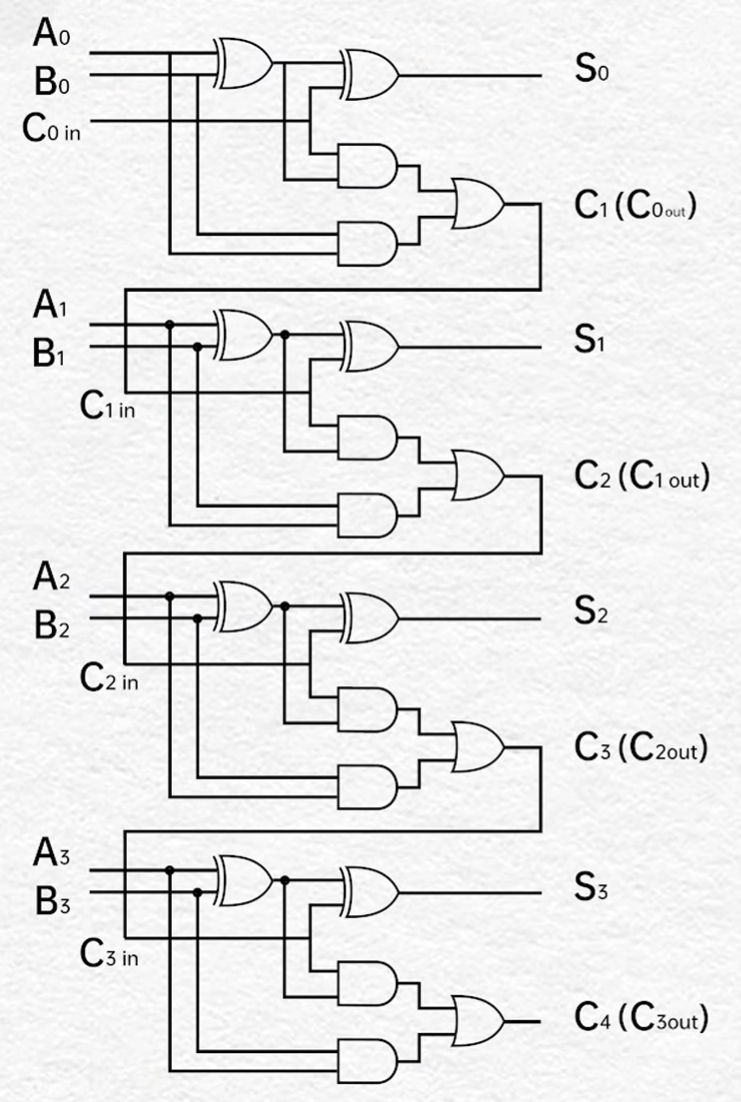
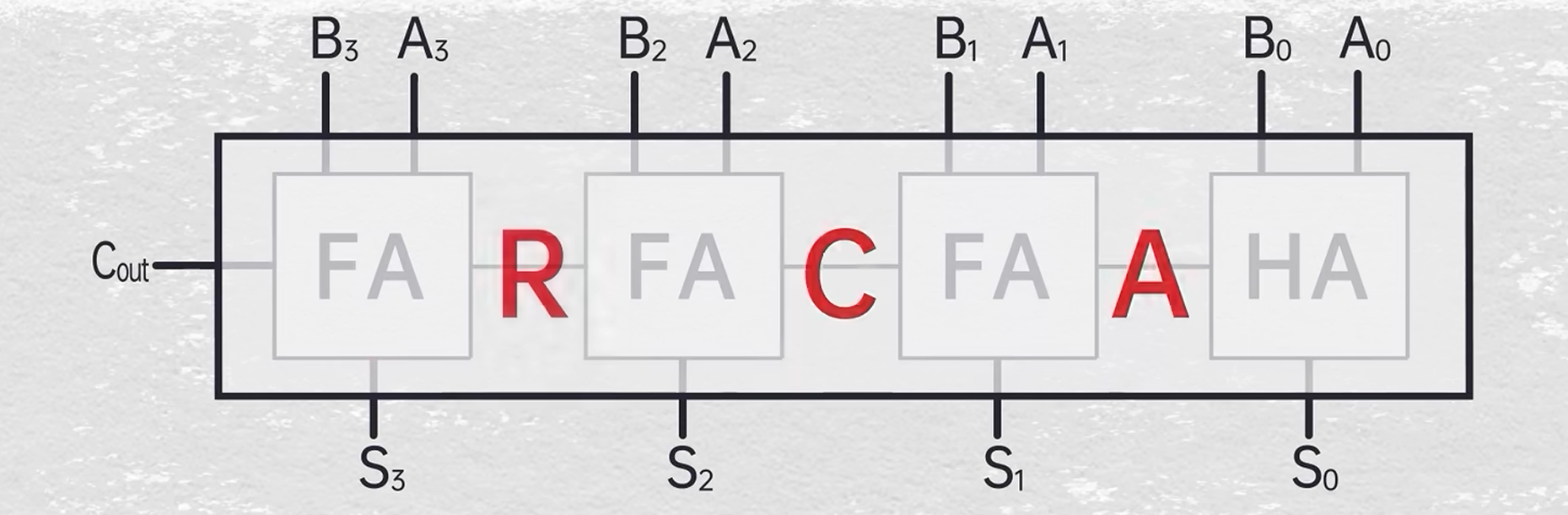
阵列乘法器

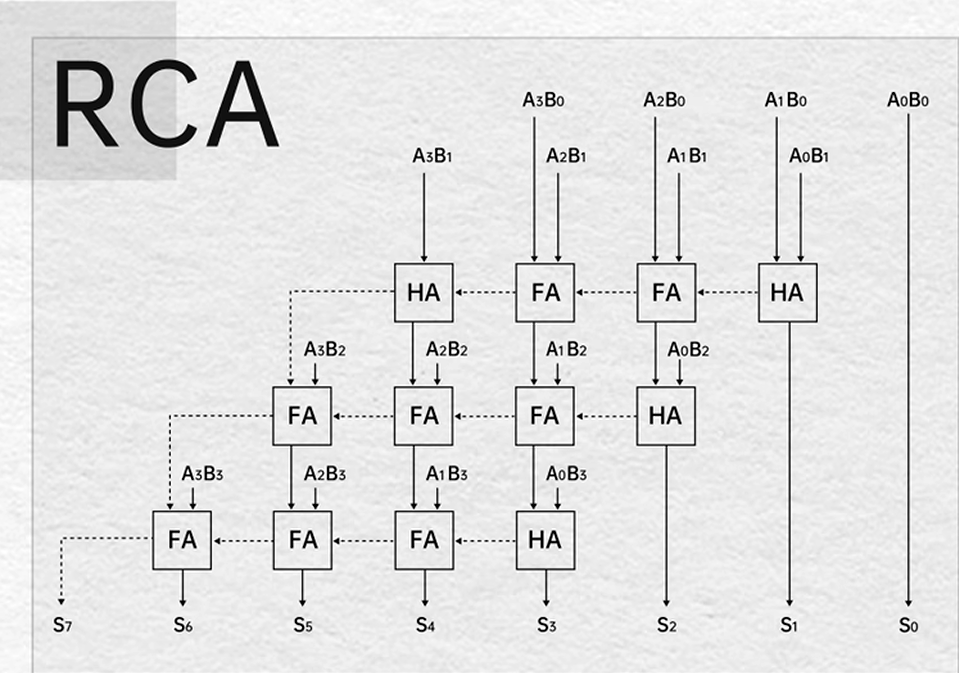
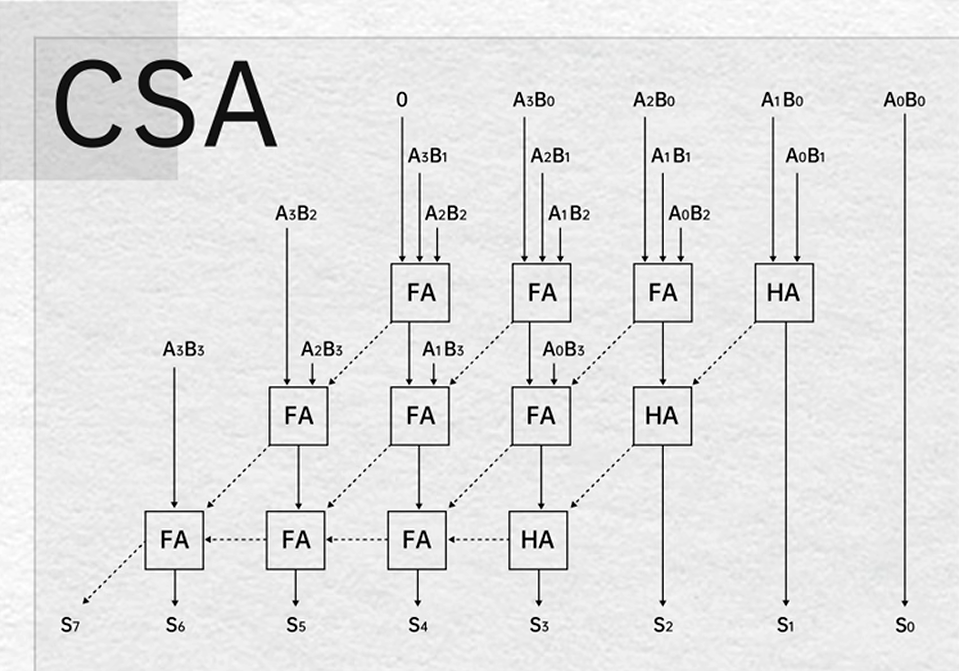
第四章存储系统

存储器基础概念

存储器分类

按存储介质：半导体、磁性材料、光、纸
按存取方式：
- 随机存储器(RAM)：存取时间与物理位置无关
- 顺序存储器：存取时间与物理位置有关(磁盘/光盘/磁带)
按读写方式：
- RAM (Random Access Memory)
- ROM (Read Only Memory)
按信息保存性：
- 永久性(非易失性)：断电不丢失
- 非永久性(易失性)：断电丢失

主存技术指标

存储容量：存储器所能存储的二进制信息位数
存取速度：
- 存取时间：启动存取操作到完成的时间
- 存储周期：连续两次存取操作的最短时间间隔
- 存储器带宽：单位时间内存取的信息位数

大端小端模式

概念

大端(big-endian)：最高字节地址作为字地址
小端(little-endian)：最低字节地址作为字地址
68000采用大端，Intel采用小端，ARM两者都支持

例题

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


例：int a = 0x12345678 在内存中的存放方式
大端模式：
0x4000: 0x12
0x4001: 0x34
0x4002: 0x56
0x4003: 0x78

小端模式：
0x4000: 0x78
0x4001: 0x56
0x4002: 0x34
0x4003: 0x12

半导体存储器

SRAM

基本存储单元结构

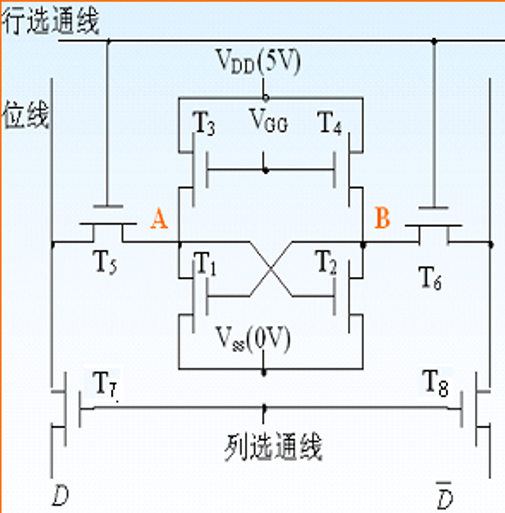
SRAM 的基本存储单元是由六个晶体管构成的双稳态触发器，通常称为"六管SRAM"或"6T SRAM"。

主要组成部分 (Main components)：

4个NMOS管和2个PMOS管
2个交叉耦合的反相器
2个访问晶体管（传输管）
1个位线对（BL和BLB）
1个字线（WL）

工作原理

SRAM的工作原理基于双稳态触发器的特性：

双稳态特性 (Bistable characteristic)：
- 两个稳定状态：‘0’和'1’
- 只要有电源供应，数据就能稳定保持
- 不需要周期性刷新
反相器对 (Inverter pair)：
- 两个反相器互连形成正反馈
- 一个节点为高电平时，另一个必为低电平
- 形成自锁回路

读写过程

写操作 (Write Operation)：

激活字线(WL)
在位线对(BL/BLB)上施加互补信号
通过访问晶体管强制改变存储节点电平
新数据被锁存

读操作 (Read Operation)：

预充电位线对至高电平
激活字线
存储单元将数据传递到位线对
感测放大器检测位线电压差
输出数据

SRAM不需要刷新的原因

SRAM不需要刷新的特点源于其结构特性：

持续性供电 (Continuous Power)：
- 只要有电源供应，数据就能稳定保持
- 交叉耦合的反相器持续维持状态
稳定性 (Stability)：
- 正反馈结构保证数据稳定
- 不存在电荷泄漏问题
- 不像DRAM需要定期刷新

DRAM

基本存储单元结构

DRAM 的基本存储单元由一个晶体管和一个电容构成，通常称为"1T1C"结构：

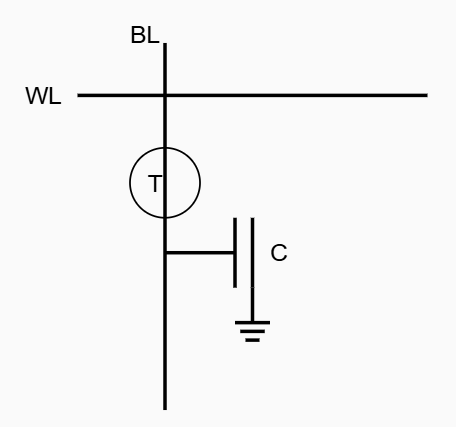
工作原理

一个晶体管一个电容

DRAM 的工作原理基于电荷存储：

数据存储：
- 1：电容充电（高电平）
- 0：电容放电（低电平）
电荷泄漏：
- 电容会随时间缓慢放电
- 需要定期刷新维持数据

读写过程

写操作 (Write Operation)：

激活字线(WL)，打开访问晶体管
在位线(BL)上施加数据电平
电容充电或放电
关闭字线，数据被存储

读操作 (Read Operation)：

位线预充电至中间电平
激活字线，打开访问晶体管
电荷共享导致位线电平变化
感测放大器检测并放大电平差
数据输出并回写（破坏性读出）

刷新操作

刷新周期 (Refresh Cycle)

标准刷新周期：2ms
在2ms内必须完成所有存储单元的刷新
刷新间隔 = 刷新周期 ÷ 行数

1
2
3
4
5
6
7
8


问：一个1024×1024的DRAM芯片，刷新周期为2ms，采用集中刷新方式，
计算刷新时间占用的百分比，假设每次刷新操作耗时100ns。

解：
1. 总行数 = 1024
2. 2ms内需要刷新1024行
3. 总刷新时间 = 1024 × 100ns = 102.4μs
4. 占用百分比 = (102.4μs ÷ 2ms) × 100% = 5.12%

刷新方式

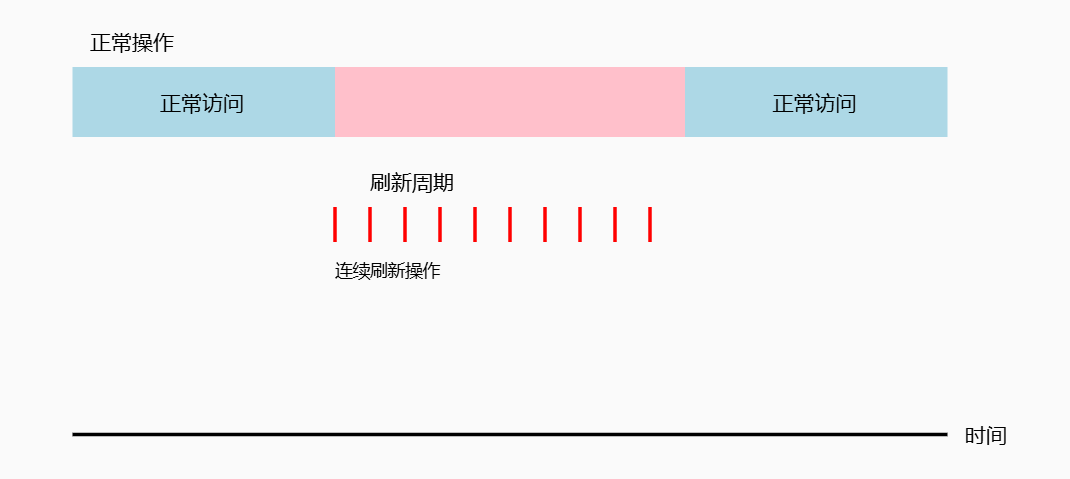
集中刷新 (Burst Refresh)

工作原理

在固定的时间段内，连续对所有行进行刷新，期间停止所有正常的存储器访问操作。

操作流程

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


1. 进入刷新周期：
   - 停止响应所有存储器访问请求
   - 将刷新计数器清零

2. 连续刷新过程：
   - 选择当前行（由刷新计数器指定）
   - 执行刷新操作
   - 刷新计数器+1
   - 重复直到所有行刷新完成

3. 退出刷新周期：
   - 恢复正常的存储器访问

时序图

例题

题目：某DRAM芯片容量为4M×8位，刷新周期要求为4ms，每次刷新操作需要100ns。该DRAM采用集中刷新方式，要求：

计算需要多少根地址线
计算总的刷新时间
计算在刷新期间的存储器利用率损失
如果CPU时钟周期为10ns，计算在一个刷新周期内损失的CPU周期数

解答：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


1. 地址线计算：
   - 总容量 = 4M×8位 = 4194304×8位
   - 行地址需要：log₂(√4194304) = 11位
   - 列地址需要：log₂(√4194304) = 11位
   - 总地址线：11 + 11 = 22根

2. 刷新时间计算：
   - 行数 = 2¹¹ = 2048行
   - 总刷新时间 = 2048行 × 100ns = 204.8μs

3. 存储器利用率损失：
   - 刷新周期 = 4ms = 4000μs
   - 利用率损失 = (204.8μs ÷ 4000μs) × 100% = 5.12%

4. 损失的CPU周期：
   - 刷新时间 = 204.8μs = 204800ns
   - 损失的CPU周期数 = 204800ns ÷ 10ns = 20480个周期

分散刷新 (Distributed Refresh)

工作原理

在每个存储器正常访问周期结束后，插入一次刷新操作。

操作流程

1
2
3
4
5
6
7
8


1. 执行正常的存储器访问操作

2. 访问周期结束后：
   - 执行一次刷新操作（刷新一行）
   - 刷新计数器+1
   - 为下一行刷新做准备

3. 开始下一个访问周期

时序图

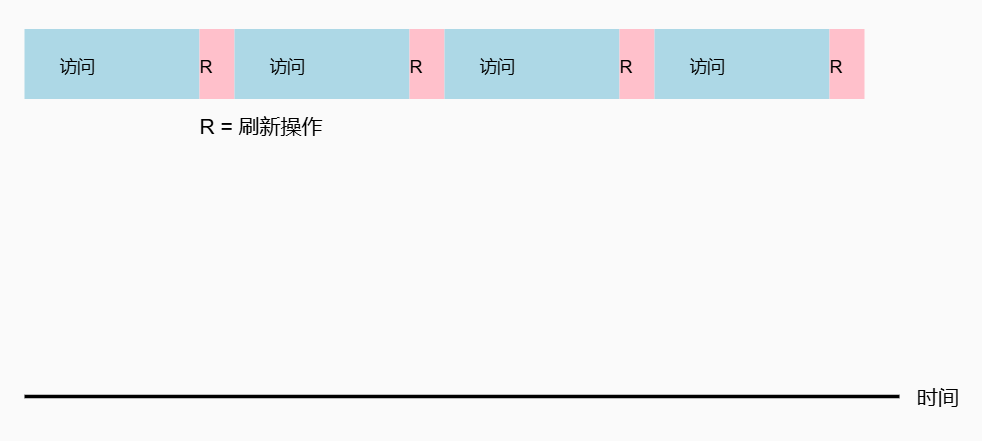
例题

题目：某DRAM芯片为16M×4位，刷新周期为2ms，采用分散刷新方式。存储器的读写周期为80ns，刷新操作需要100ns。请计算：

一个完整的存储器周期时间
实际的存储器带宽
如果改用集中刷新，两种方式的存储器利用率比较
刷新操作的频率

解答：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


1. 存储器周期计算：
   - 行数 = √(16M) = 4096行
   - 每个刷新周期内需要刷新次数 = 4096次
   - 每次刷新间隔 = 2ms ÷ 4096 ≈ 488ns
   - 完整周期 = 80ns(读写) + 100ns(刷新) = 180ns

2. 实际带宽计算：
   - 理论周期时间 = 80ns
   - 实际周期时间 = 180ns
   - 理论带宽 = (4位 ÷ 80ns) = 50MB/s
   - 实际带宽 = (4位 ÷ 180ns) ≈ 22.22MB/s

3. 刷新方式比较：
   分散刷新：
   - 利用率 = 80ns ÷ 180ns ≈ 44.4%

   集中刷新：
   - 总刷新时间 = 4096 × 100ns = 409.6μs
   - 利用率 = (2000μs - 409.6μs) ÷ 2000μs ≈ 79.52%

4. 刷新频率：
   - 每488ns进行一次刷新
   - 刷新频率 = 1 ÷ 488ns ≈ 2.049MHz

异步刷新 (Asynchronous Refresh)

工作原理

将刷新周期分成多个时间片，每个时间片内完成部分行的刷新。

操作流程

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


1. 刷新周期分段：
   - 通常分为8个或16个时间片
   - 每个时间片负责特定数量的行刷新

2. 每个时间片内：
   - 连续刷新分配给该时间片的所有行
   - 其他时间用于正常访问

3. 时间片切换：
   - 完成当前时间片的刷新任务
   - 等待下一个时间片

时序图

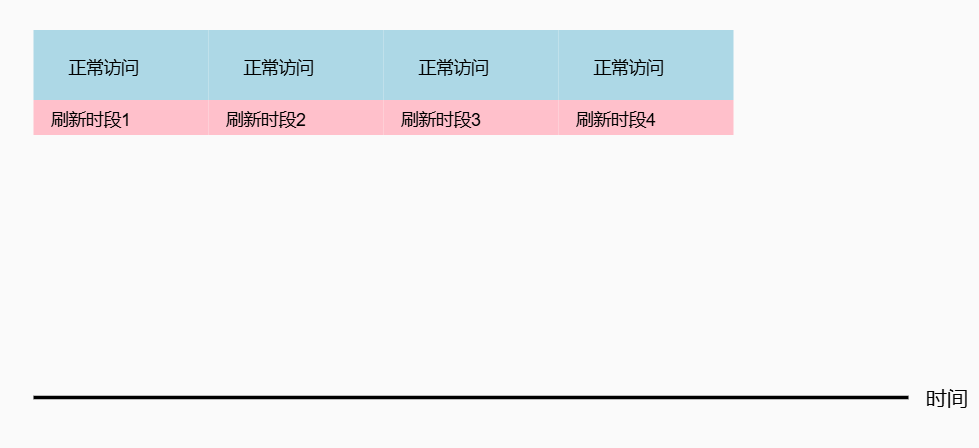
异步刷新例题

题目：某DRAM容量为64M×8位，刷新周期4ms，采用异步刷新方式，将刷新周期分为8个时间片。每次刷新操作需要120ns，普通读写操作需要100ns。请计算：

每个时间片的持续时间和需要刷新的行数
每个时间片内的存储器利用率
如果要求系统响应时间不超过1μs，判断是否满足要求
计算平均访问时间

解答：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


1. 时间片计算：
   - 总行数 = √64M = 8192行
   - 每个时间片时长 = 4ms ÷ 8 = 500μs
   - 每个时间片需刷新行数 = 8192 ÷ 8 = 1024行
   - 每个时间片的刷新时间 = 1024 × 120ns = 122.88μs

2. 存储器利用率：
   - 每个时间片可用时间 = 500μs - 122.88μs = 377.12μs
   - 单片利用率 = 377.12μs ÷ 500μs ≈ 75.424%

3. 响应时间分析：
   - 最坏情况：刷新操作正在进行时收到访问请求
   - 最大等待时间 = 1024行 × 120ns = 122.88μs
   - 122.88μs > 1μs，不满足要求

4. 平均访问时间：
   - 正常访问时间 = 100ns
   - 刷新影响时间 = (122.88μs ÷ 500μs) × 100ns = 24.576ns
   - 平均访问时间 = 100ns + 24.576ns = 124.576ns

三种方式的比较

特性	集中刷新	分散刷新	异步刷新
控制复杂度	简单	复杂	中等
存储器利用率	低	高	中等
实现难度	容易	困难	中等
刷新效率	高	低	中等
对系统影响	大	小	中等

主存与CPU的连接

存储器扩展

位扩展 (Bit Extension)

当存储器的数据位宽不足以满足系统需求时，需要进行位扩展。

原理 (Principle)

将多个存储器芯片并联，增加数据位宽
所有芯片共用相同的地址线和控制线
每个芯片负责存储数据的不同位

示例 (Example)

将两个8位宽的存储器芯片组成16位宽的存储器：

芯片1：存储D0-D7
芯片2：存储D8-D15
共用地址线A0-An
共用片选信号CS、读写控制信号R/W

字扩展 (Word Extension)

当存储器容量（字数）不足时，需要进行字扩展。

原理 (Principle)

将多个存储器芯片串联，增加存储容量
所有芯片共用数据线和控制线
通过片选信号选择不同的芯片

示例 (Example)

将两个1K×8位的存储器组成2K×8位的存储器：

使用A10作为片选信号
A10=0选择芯片1（地址0-1023）
A10=1选择芯片2（地址1024-2047）

字位同时扩展 (Word-Bit Simultaneous Extension)

当需要同时扩展数据位宽和存储容量时使用。

原理 (Principle)

结合位扩展和字扩展的方法
形成一个矩阵式的存储器阵列
需要同时考虑数据位的分配和片选逻辑

示例 (Example)

用4个1K×8位的存储器组成2K×16位的存储器：

水平方向：位扩展（8位→16位）
垂直方向：字扩展（1K→2K）

片选方式 (Chip Selection Methods)

线选法 (Linear Selection)

线选法是最简单的片选方式，直接用一根选通线来选中一个存储芯片。每个存储芯片都有独立的片选信号线。

优点：
- 电路简单，容易实现
- 选择速度快
缺点：
- 需要的片选线数量多
- 当存储芯片数量增加时，占用的I/O端口也相应增加
- 扩展能力受限
全译码法 (Full Decoding)

全译码法使用地址译码器将n位二进制地址译码成$2^n$个片选信号。

优点：
- 片选线使用效率高
- 每个地址都对应唯一的存储芯片
- 地址空间利用率100%
特点：
- n根地址线可以选择$2^n$个存储芯片
- 需要使用译码器（如74138）
- 地址连续，没有空隙
部分译码法 (Partial Decoding)

部分译码法只使用地址的部分位进行译码，一个片选信号可能对应多个地址。

优点：
- 电路比全译码简单
- 需要的译码器更少
- 适合于地址空间不需要完全使用的场合
缺点：
- 地址空间有重复
- 存储器的编址不连续
- 地址空间利用率低

例题

例1（字扩展）：用16K8位的芯片，去构造内存64K8，并要完成与CPU的对接，并求出每一个芯片在全局空间中的地址范围。

解答：

需要的芯片数量：
1

64K ÷ 16K = 4片芯片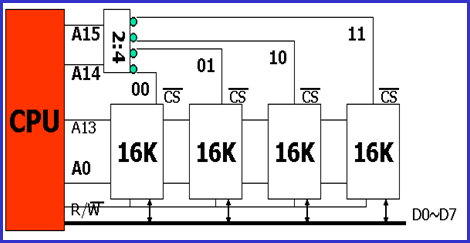

地址范围：

总地址范围：0000H ~ FFFFH (64K = 2^16)
每片芯片负责16K地址空间
16K = 16384 = 4000H

地址分配表 / Address Allocation Table

芯片号/No.	地址范围 / Address Range	16进制值/Hex Value
	A15 A14 A13~A0
0	0 0 0000~3FFF	00000H ~ 03FFFH
1	0 1 0000~3FFF	04000H ~ 07FFFH
2	1 0 0000~3FFF	08000H ~ 0BFFFH
3	1 1 0000~3FFF	0C000H ~ 0FFFFH

解释说明 / Explanation

地址线分配 / Address Line Assignment:
- A15, A14：用于片选（选择哪个芯片）
- A13~A0：用于芯片内部寻址（14位）
片选逻辑 / Chip Selection Logic:
- 芯片0：当A15=0, A14=0时选中
- 芯片1：当A15=0, A14=1时选中
- 芯片2：当A15=1, A14=0时选中
- 芯片3：当A15=1, A14=1时选中
地址范围计算 / Address Range Calculation:
- 每片芯片负责16K (4000H) 的地址空间
- 芯片0：0000H ~ 3FFFH
- 芯片1：4000H ~ 7FFFH
- 芯片2：8000H ~ BFFFH
- 芯片3：C000H ~ FFFFH

例2（位扩展）：用256K ×8位的存储体构造 2M × 32位的存储器，并完成与CPU的连接

先用4片256K X 8位的存储体构成 256K X 32的存储体
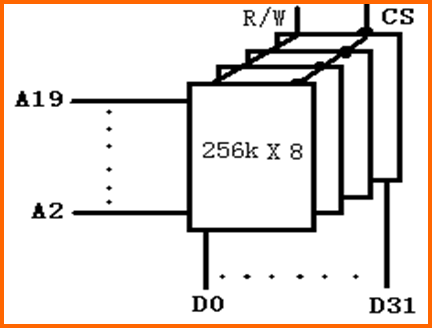
然后和字扩展一样

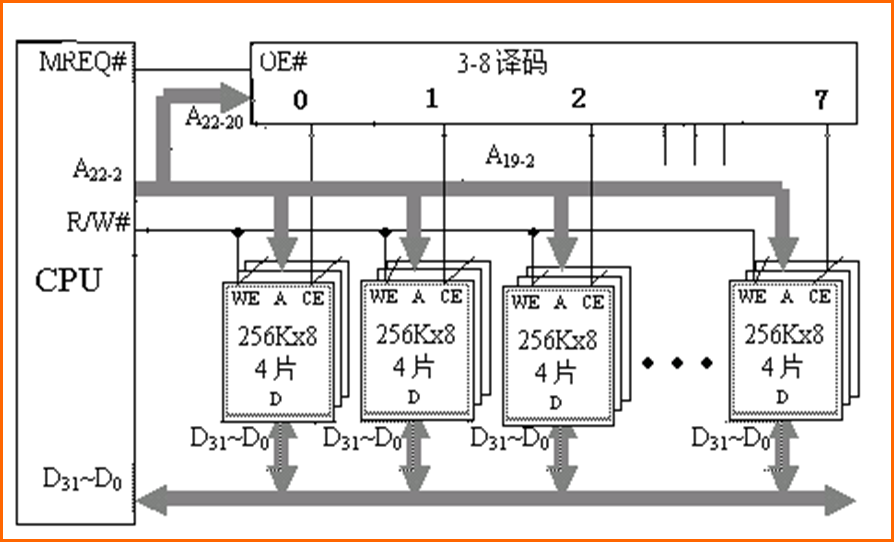
Cache

工作原理 / How Cache Works

数据存储：
- Cache将最常用的数据从主存复制到高速缓存中
- 按照块（Block）或行（Line）为单位进行存储
访问过程：
- CPU首先查找数据是否在Cache中（Cache命中）
- 如果命中（Hit），直接从Cache读取
- 如果未命中（Miss），从主存读取并放入Cache
替换策略：
- 当Cache满时，需要决定替换哪些数据
- 常见策略包括LRU（最近最少使用）、FIFO（先进先出）等

局局部性原理 / Principle of Locality

时间局部性 / Temporal Locality
- 定义：如果一个数据被访问，那么在近期它很可能再次被访问
- 例子：
  - 循环中的变量
  - 频繁调用的函数
  - 计数器
1 2 3

for(int i = 0; i < 100; i++) { // i具有很好的时间局部性 sum += array[i]; }
空间局部性 / Spatial Locality
- 定义：如果一个数据被访问，那么它周围的数据很可能也会被访问
- 例子：
  - 数组的连续访问
  - 顺序执行的指令
  - 结构体中的相邻成员
1 2 3 4

int array[100]; for(int i = 0; i < 100; i++) { array[i] = i; // 数组连续访问体现了空间局部性 }

局部性原理的重要性 / Importance of Locality

性能优化：
- 利用局部性原理可以提高Cache命中率
- 减少主存访问次数，提升系统性能
程序设计：
- 影响程序编写方式
- 引导更好的数据结构和算法选择

实际应用示例 / Practical Example

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


// 体现良好局部性的代码
for(int i = 0; i < N; i++) {
    for(int j = 0; j < N; j++) {
        array[i][j] = 0;  // 按行访问，具有好的空间局部性
    }
}

// 较差局部性的代码
for(int j = 0; j < N; j++) {
    for(int i = 0; i < N; i++) {
        array[i][j] = 0;  // 按列访问，空间局部性较差
    }
}

这个例子展示了如何通过合适的访问模式来利用空间局部性，提高程序性能。第一种方式（按行访问）能更好地利用Cache的特性，而第二种方式（按列访问）会导致更多的Cache未命中。

存储器映射方式 Memory Mapping Methods

直接映射 (Direct Mapping)
- 基本概念
  
  直接映射是最简单的映射方式，主存中的每个块只能映射到Cache中的一个特定位置。
- 地址结构
  
  主存地址分为三个字段：
  - 标记(Tag)：用于识别是否是所需的块
  - 组号/行号(Line)：确定Cache中的位置
  - 块内地址(Block Offset)：确定块内的具体单元
- 例题 Example
  
  假设有一个存储系统具有以下参数：
  - 主存容量：1024KB = 2^20 B
  - Cache容量：16KB = 2^14 B
  - 块大小：64B = 2^6 B
  解答：
  1. 计算地址位数：
    - 主存地址位数 = log2(1024×1024) = 20位
  2. 计算各字段位数：
    - 块内地址：log2(64) = 6位
    - Cache行数：16KB/64B = 256行，所以行号需要8位
    - 标记位：20 - 8 - 6 = 6位
  3. 地址格式：
  1
  
  | 标记(6位) | 行号(8位) | 块内地址(6位) |
全相联映射 (Fully Associative Mapping)
- 基本概念 Basic Concept
  
  主存中的任何一块可以映射到Cache中的任何位置。需要并行对比所有Cache行。
- 地址结构 Address Structure
  
  主存地址分为两个字段：
  - 标记(Tag)
  - 块内地址(Block Offset)
- 例题 Example
  
  使用上述相同参数，求地址格式。
  
  解答
```
1. 块内地址：同样是6位
2. 标记位：
    - 不需要行号字段
    - 标记位 = 20 - 6 = 14位
3. 地址格式：

```
  |    标记(14位)    |  块内地址(6位)  |
```
```
组相联映射 (Set Associative Mapping)
- 基本概念 Basic Concept
  
  是直接映射和全相联映射的折中方案。Cache分成若干组，每组包含n个行（n路组相联）。
- 地址结构 Address Structure
  
  主存地址分为三个字段：
  - 标记(Tag)
  - 组号(Set)
  - 块内地址(Block Offset)
- 例题 Example
  
  假设采用4路组相联，其他参数同上。
  
  解答：
```
1. 计算组数：
    - 总行数 = 256行
    - 每组4行
    - 组数 = 256/4 = 64组
2. 计算各字段位数：
    - 块内地址：6位
    - 组号：log2(64) = 6位
    - 标记位：20 - 6 - 6 = 8位
3. 地址格式：

```
  |  标记(8位)  |  组号(6位)  |  块内地址(6位)  |
```
```

性能比较 Performance Comparison

命中率 Hit Rate：
- 全相联 > 组相联 > 直接映射
硬件复杂度 Hardware Complexity：
- 直接映射 < 组相联 < 全相联
查找速度 Search Speed：
- 直接映射 > 组相联 > 全相联

综合例题 Comprehensive Example

假设主存地址为32位，Cache大小为64KB，块大小为32B，采用8路组相联映射，求：

地址格式
Cache总行数
每组行数
组数
标记位、组号位、块内地址位的位数

解答 Solution:

Cache总行数：
- 64KB/32B = 2048行
每组行数：
- 8行（8路组相联）
组数：
- 2048/8 = 256组
地址位的分配：
- 块内地址：log2(32) = 5位
- 组号：log2(256) = 8位
- 标记：32 - 8 - 5 = 19位
地址格式：

1

|    标记(19位)    |  组号(8位)  |  块内地址(5位)  |

替换算法

LRU

工作原理
- 替换最长时间没有被访问的数据块
- 需要记录每个数据块的最后访问时间
- 基于程序的时间局部性原理
实现方式
- 计数器法：记录上次访问时间
- 栈实现：最近使用的放栈顶
- 链表实现：访问后移至表头

例题

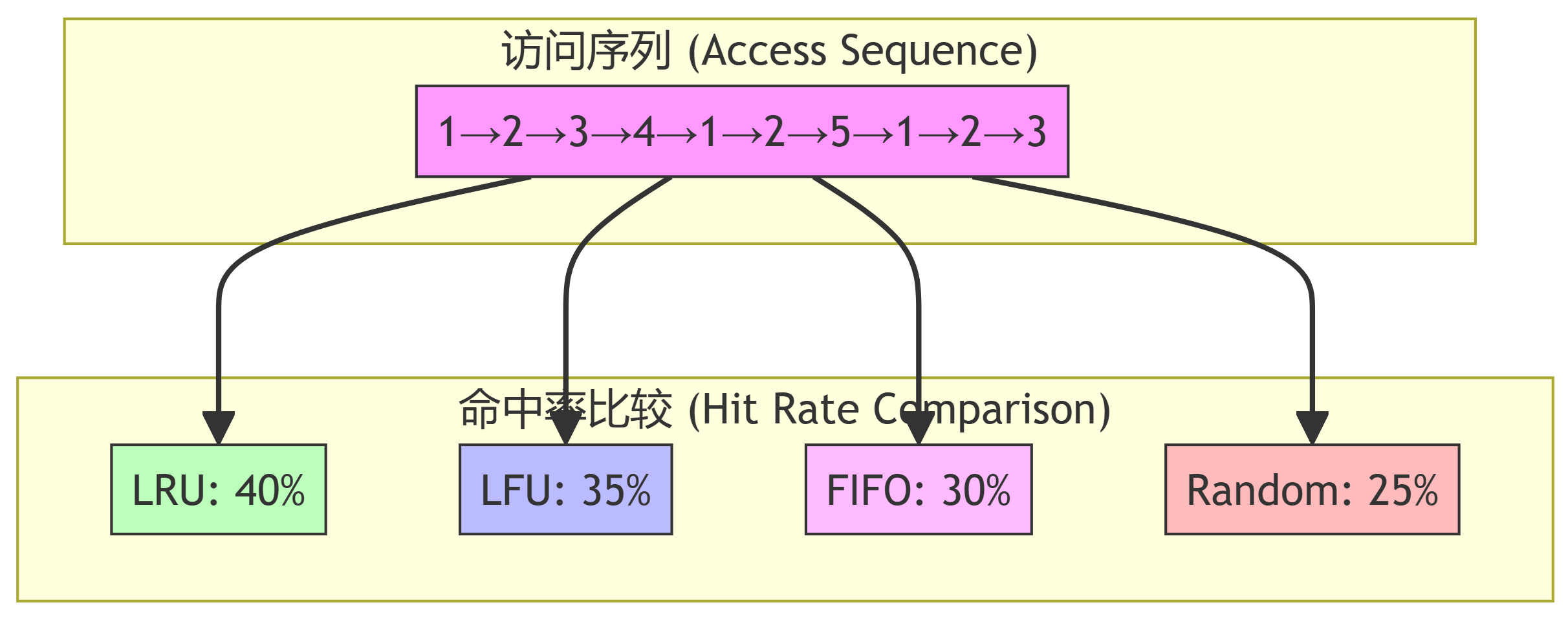
假设有一个容量为 3 的 Cache，访问序列为：1, 2, 3, 4, 1, 2, 5, 1, 2, 3

1
2
3
4
5
6
7
8


初始状态：[ ][ ][ ]
1 访问 → [1][ ][ ]
2 访问 → [2][1][ ]
3 访问 → [3][2][1]
4 访问 → [4][3][2]    (替换最久未使用的1)
1 访问 → [1][4][3]    (替换最久未使用的2)
2 访问 → [2][1][4]    (替换最久未使用的3)
5 访问 → [5][2][1]    (替换最久未使用的4)

LFU

工作原理
- 替换访问次数最少的数据块
- 需要维护访问计数器
- 基于使用频率进行判断

例题

假设有一个容量为 3 的 Cache，访问序列为：1, 1, 1, 2, 2, 3, 4, 1

1
2
3
4
5
6
7
8


初始状态：[ ][ ][ ]
1 访问 → [1:1][ ][ ]       (数字:计数)
1 访问 → [1:2][ ][ ]
1 访问 → [1:3][ ][ ]
2 访问 → [1:3][2:1][ ]
2 访问 → [1:3][2:2][ ]
3 访问 → [1:3][2:2][3:1]
4 访问 → [1:3][2:2][4:1]  (替换计数最小的3)

FIFO

工作原理
- 替换最早进入 Cache 的数据块
- 类似队列操作
- 实现简单，硬件开销小

例题

假设有一个容量为 3 的 Cache，访问序列为：1, 2, 3, 4, 2, 1, 5

1
2
3
4
5
6
7
8


初始状态：[ ][ ][ ]
1 进入 → [1][ ][ ]
2 进入 → [1][2][ ]
3 进入 → [1][2][3]
4 进入 → [4][2][3]    (替换最早进入的1)
2 访问 → [4][2][3]    (已存在，不变)
1 进入 → [4][2][1]    (替换最早进入的3)
5 进入 → [4][5][1]    (替换最早进入的2)

随机替换

工作原理
- 随机选择要替换的数据块
- 不需要维护任何历史信息
- 硬件实现最简单

例题

假设有一个容量为 3 的 Cache，访问序列为：1, 2, 3, 4, 2, 1, 5

过程演示 (Process Demonstration)

1
2
3
4
5
6
7
8


初始状态：[ ][ ][ ]
1 进入 → [1][ ][ ]
2 进入 → [1][2][ ]
3 进入 → [1][2][3]
4 进入 → [4][2][3]    (随机替换了1)
2 访问 → [4][2][3]    (已存在，不变)
1 进入 → [4][1][3]    (随机替换了2)
5 进入 → [4][1][5]    (随机替换了3)

性能比较

写策略

写直达法(Write Through)

数据同时写入 Cache 和主存
每次写操作都要访问主存
Cache 和主存的数据始终保持一致

写回法(Write Back)

写操作只修改 Cache 中的数据
被修改的数据块被标记为"脏"(dirty)
当脏块被替换时，才写回主存

性能计算

命中率计算

在一个程序执行期间，设$N_c$表示Cache完成存取的总次数，$N_m$表示主存完成存取的总次数，h定义为命中率，则有

$$ h=\frac{N_c}{N_c+N_m} $$

平均访问时间计算

若$t_c$表示命中时的Cache访问时间，$t_m$表示未命中时的主存访问时间，$1-h$表示未命中率，则Cache/主存系统的平均访问时间$t_a$为

$$ t_a=h\cdot t_c+(1-h)t_m　 $$

Cache效率计算

设$r=\frac{tm}{tc}$表示主存慢于Cache的倍率,e表示访问效率，则有:

$$ e = \frac{t_c}{t_a} = \frac{t_c}{ht_c + (1-h)t_m} = \frac{1}{r + (1-r)h} = \frac{1}{h + (1-h)r} $$

第一章 计算机系统概论

计算机发展历程

计算机的四代发展

计算机系统的层次结构

计算机系统的五个层次

性能指标

主要性能指标

CPI(Cycles Per Instruction)

MIPS(Million Instructions Per Second)

重要例题分析

例题1: CPI计算

例题2: CPU性能计算

例题3: MIPS计算

冯·诺依曼计算机的基本特点

第二章 计算机数据表示

数据表示基础

为什么使用二进制

数据表示考虑因素

数值数据表示

机器数的编码方式

原码

反码

补码

移码

例题

示例1：将十进制数 +52 转换为8位二进制机器码

示例2：将十进制数 -52 转换为8位二进制机器码

转换口诀

整型和浮点型表示

整型

浮点数

例子：存储float类型的12.375

字节序

数据校验

码距

奇偶校验

偶校验 / Even Parity

奇校验 / Odd Parity

海明码

校验码位置

校验码数量

校验码负责校验的位置

校验码的值

对单个错误进行纠错

例题 海明码实例：4位数据的(7,4)海明码

CRC循环冗余校验

校验流程

CRC循环校验的优势和劣势

例题 CRC计算

第三章 运算方法与运算器

定点加减法运算

补码加法运算 (Addition in Two’s Complement)

补码减法运算 (Subtraction in Two’s Complement)

溢出检测 (Overflow Detection)

检测方法 (Detection Methods)

补码的加减法示例 (Examples)

定点乘法运算

原码乘法运算

补码乘法运算（Booth算法）

补码乘法小数位置确定

定点除法运算

原码除法运算

恢复余数除法

补码的除法运算

运算步骤

浮点数加减法

运算步骤

示例 Examples

例1：基本加法 Basic Addition

例2：异号加法（实质是减法）Subtraction

特殊情况 Special Cases

运算方法与运算器

半加法器（Half Adder HA）

全加法器（Full Adder FA）

串行进位全加法器

阵列乘法器

第四章 存储系统

存储器基础概念

存储器分类

主存技术指标

第一章计算机系统概论

第二章计算机数据表示

例题海明码实例：4位数据的(7,4)海明码

第三章运算方法与运算器

第四章存储系统